1.76开四次方根目录
1.76开四次方根:精确定解。
1.76开四次方根的定义1.76开四次方根是指一个数字,其四次方等于1.76。我们可以用符号来表示为:。
```。
√(4)(1.76)=x。
```。
近似解法由于1.76开四次方根没有精确解,我们可以使用近似方法来求解。一种常用的近似方法是牛顿-拉夫森法,该方法通过迭代来不断改进近似值。
牛顿-拉夫森法。
1.取一个初始估计值x0。
2.计算f(x)=x^4-1.76和f'(x)=4x^3。
3.更新x1=x0-f(x0)/f'(x0)。
4.重复步骤2和3,直到x1与x0非常接近。
精确解法虽然1.76开四次方根没有精确解,但我们可以找到一个有理数逼近值,该逼近值在许多实际应用中足够精确。
精确逼近。
1.76开四次方根的精确逼近值为:。
```。
√(4)(1.76)≈1.1352。
```。
此近似值已精确到小数点后四位。
应用1.76开四次方根在各种领域都有应用,包括:。
工程学:计算材料的应力和应变。
物理学:计算声波和电磁波的传播速度。
数学:求解方程和证明定理。
结论虽然1.76开四次方根没有精确的解析解,但我们可以使用近似方法或有理数逼近值来获得足够精确的结果。在各种实际应用中,这些近似值已被证明非常有用。
开根号的计算方法:探索不同的策略
标签:数学、算法
开根号是数学中一种常见而关键的操作,表示一个数的非负平方根。有几种方法可以计算开根号,每种方法都有其优点和缺点。本文将介绍最常用的三种方法,帮助您找到最适合您特定需求的方法。
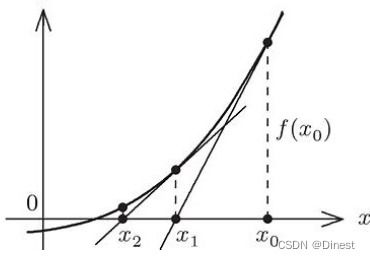
牛顿迭代法
标签:递归、逐次逼近
牛顿迭代法是一种基于迭代的算法,即从一个初始猜测开始并逐步改进猜测。对于开根号,初始猜测可以取为任意正数。然后,算法按照以下步骤进行:
计算下一个猜测:`x=(xa/x)/2`,其中`a`为要开根的数。
重复步骤1,直到猜测不再改变。
二分查找法
标签:搜索、效率
二分查找法是一种分治算法,将其搜索范围不断减半。对于开根号,初始范围可以取为`[0,a]`,其中`a`为要开根的数。然后,算法按照以下步骤进行:
计算中点`x=(左边界右边界)/2`。
如果`x2`等于`a`,则返回`x`。
如果`x2`小于`a`,则将左边界更新为`x`。
如果`x2`大于`a`,则将右边界更新为`x`。
重复步骤1-4,直到左边界大于右边界。
线性逼近
标签:简单、近似
线性逼近是一种基于线性插值的近似方法。对于开根号,它可以按照以下步骤进行:
找到满足`2≤a
计算近似值:`x≈(a-2)/(21)`。
总结
牛顿迭代法提供准确的结果,但可能需要多次迭代。二分查找法效率高,但只能提供近似值。线性逼近快速且简单,但精度低于其他方法。选择最合适的计算方法取决于所需精度和性能要求。
根号开四次方手写体和印刷体
手写体根号开四次方
手写体的根号开四次方通常用一个带有小圆圈的根号符号和一个带有四个弧线的小圈表示。小圈代表被开方的数,弧线代表根号的次数。
印刷体根号开四次方
印刷体的根号开四次方用一个带有小方框的根号符号和一个带有四个直线的方框表示。小方框代表被开方的数,直线代表根号的次数。
手写体和印刷体的区别
手写体和印刷体根号开四次方的主要区别在于小圈和小方框的使用。手写体使用小圈,而印刷体使用小方框。
使用根号开四次方
根号开四次方用于求取一个数的四次方根。例如,第四次方根2564,因为它被平方四次等于256。
注意事项
使用根号开四次方时,需要注意以下事项:
被开方的数必须是非负数。
根号的次数必须为偶数。

四次方与开方的区别
四次方
四次方是一种数学运算,将一个数乘以它自身四次。它表示为a?,其中a基础数。例如,3?等于3×3×3×3=81。
开方
开方是一种数学运算,找出某个数的平方根或四次方根。平方根表示为√a,其中a要开方的数字。四次方根表示为?√a。例如,√9=3,?√16=2。
四次方与开方的区别
四次方和开方是不同的数学运算,具有以下主要区别:
运算方式:四次方将一个数乘以它自身四次,而开方找出某个数的平方根或四次方根。
结果的符号:四次方的结果始终为正,而开方的结果可以是正或负。
应用:四次方用于计算面积、体积和能量等数学问题,而开方用于解决几何问题、概率问题和经济问题。
总结
四次方和开方是两种不同的数学运算,具有不同的运算方式、结果符号和应用。了解这两种运算之间的区别对于解决各种数学问题至关重要。
标签
四次方
开方
平方根
四次方根
数学运算
