标准正态分布，也称为高斯分布或钟形曲线，是概率论和统计学中的一个重要概念。它描述了一个连续随机变量在某个平均值周围对称分布的情况。标准正态分布的均值（μ）为0，标准差（σ）为1。这意味着大多数数据点将集中在均值附近，且数据点随着距离均值的增加而迅速减少。

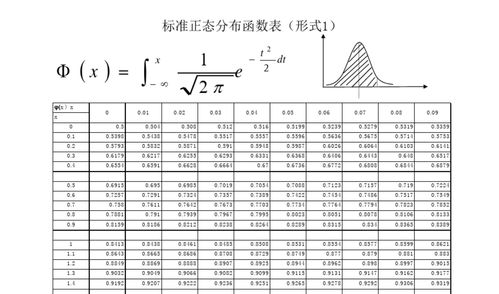
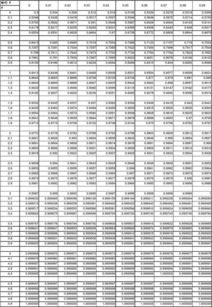
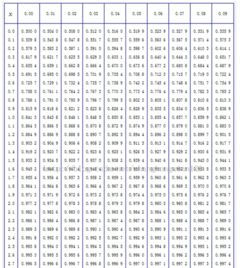
在标准正态分布中，一个特定的z值（也称为标准分数）表示一个数据点距离均值的标准化距离。例如，z=1.76表示一个数据点比均值高出1.76个标准差。要计算z=1.76时的累积概率，可以使用标准正态分布表或相应的统计软件。

在标准正态分布中，z值越大，对应的累积概率也越大。例如，z=1.76的累积概率大约为0.9608，这意味着在标准正态分布中，大约有96.08的数据点位于z=1.76以下。

请注意，这里提供的信息仅供参考，如果您需要进行更精确的计算或深入的分析，建议使用专业的统计软件或咨询统计专家。你知道吗？在概率论的世界里，有一种分布，它就像是大自然的秘密信使，悄无声息地传递着各种信息。它就是——标准正态分布。今天，就让我带你一起揭开它的神秘面纱，看看这个“1.76”背后的故事。

标准正态分布：揭秘概率的钟形曲线

标准正态分布，又被称为u分布，它是一种以0为均值、以1为标准差的正态分布。简单来说，它就是正态分布的一个特例，就像是一个完美的标准模板。而“1.76”这个数字，则是标准正态分布中的一个关键点。

标准正态分布的起源：从高斯到现代

标准正态分布的起源可以追溯到18世纪德国数学家卡尔·弗里德里希·高斯。高斯发现，许多自然现象，如测量误差、人的身高、考试分数等，都服从正态分布。这种分布的特点是，数据集中在平均值附近，两端逐渐减少，形成一个钟形曲线。

随着时间的推移，标准正态分布逐渐成为统计学和概率论中的基石。它不仅帮助我们理解自然现象，还广泛应用于各个领域，如医学、工程、经济学等。

标准正态分布的“1.76”之谜

那么，这个“1.76”究竟是什么意思呢？其实，它代表了标准正态分布中的一个重要概念——z分数。

z分数，也称为标准化分数，它表示一个数值与平均值的差距，用标准差来衡量。在标准正态分布中，z分数为1.76的数值，意味着这个数值比平均值高出1.76个标准差。

这个概念在统计学中非常有用。比如，在医学领域，医生可以通过计算患者的z分数，来判断患者的健康状况是否正常。在经济学领域，分析师可以通过计算股票价格的z分数，来判断股票价格是否偏离了正常水平。

标准正态分布的应用：无处不在的“1.76”

标准正态分布的应用非常广泛。以下是一些常见的应用场景：

1.医学领域：医生可以通过计算患者的z分数，来判断患者的健康状况是否正常。例如，身高、体重等指标都可以通过标准正态分布来评估。

2.心理学领域：心理学家可以通过计算测试分数的z分数，来判断测试结果是否在正常范围内。

3.工程领域：工程师可以通过计算产品尺寸的z分数，来判断产品是否符合标准。

4.经济学领域：分析师可以通过计算股票价格的z分数，来判断股票价格是否偏离了正常水平。

5.统计学领域：标准正态分布是统计学中的基本概念，广泛应用于各种统计方法，如假设检验、置信区间等。

：标准正态分布的“1.76”之旅

通过这篇文章，我们了解了标准正态分布的起源、特点和应用。而“1.76”这个数字，则是标准正态分布中的一个关键点，它代表着数据与平均值的差距。在各个领域，标准正态分布都发挥着重要的作用，帮助我们更好地理解世界。所以，下次当你看到“1.76”这个数字时，不妨想想它背后的故事，感受一下概率论的神奇魅力。